Direct and Inverse Proportion

In mathematics, two variables are proportional if a change in one is always accompanied by a change in the other, and if the changes are always related by use of a constant. The constant is called the coefficient of proportionality or proportionality constant. Alternatively, we can say that one of the variables is proportional to the other.

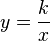
• If one variable is always the product of the other and a constant, the two are said to be directly proportional. x and y are directly proportional if the ratio is constant.
• If the product of the two variables is always equal to a constant, the two are said to be inversely proportional. x and y are inversely proportional if the product is constant.

The difference between direct and inverse proportion is pretty simple. When two things are in direct proportion that means when "A" goes up, so does "B" and in the same proportion. For example, when gas goes up, so does the cost of groceries. The cost of groceries goes up all around because of the cost of gas. The amount of gas it takes to bring the groceries to the store divided by the
amount of groceries is the increase. When you have an inverse proportion the two items go in different directions. Let's say you work in an ice cream store and you only have enough ice cream to sell 1000 scoops. The more scoops you use for bowls is inverse in proportion to the scoops you can use for cones. If you sell 750 scoops worth of ice cream in bowls, you only have 250 left for cones. If the number of scoops used in bowls goes down, the scoops for cones goes up.

The following is an example of inverse proportion:

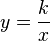
Note: k is the constant of proportionality

The following is an example of direct proportion:

Note: k is the constant of proportionality